Las Leyes de Newton
Las leyes de Newton,
también conocidas como leyes del movimiento de Newton, son tres principios a partir de los cuales se explican
la mayor parte de los problemas planteados por la mecánica, en particular, aquellos relativos al movimiento de los cuerpos. Revolucionaron los conceptos básicos de
la física y el movimiento de los cuerpos en el universo.

En concreto, la relevancia de estas leyes radica en dos aspectos:
- Por un lado, constituyen, junto con la transformación de Galileo, la base de la mecánica clásica;
- Por otro, al combinar estas leyes con la Ley de la gravitación universal, se pueden deducir y explicar las Leyes de Kepler sobre el movimiento planetario.
Así, las Leyes de Newton permiten explicar tanto el movimiento de los astros, como los movimientos de los proyectiles artificiales creados por el ser humano, así como toda la mecánica de funcionamiento de las máquinas.
Primera Ley:
La primera ley del movimiento rebate la idea aristotélica de que un cuerpo sólo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:
Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él.5
La formulación original en latín de Newton de esta ley fue:
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare6
 Esta ley postúla, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuyo resultante no sea nulo sobre él. Newton toma en cuenta, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como esta a la fricción.
Esta ley postúla, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuyo resultante no sea nulo sobre él. Newton toma en cuenta, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como esta a la fricción.
En consecuencia, un cuerpo con movimiento rectilíneo uniforme implica que no existe ninguna fuerza externa neta o, dicho de otra forma; un objeto en movimiento no se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta.
Segunda Ley:
La segunda ley del movimiento de Newton dice:
El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.
En las palabras originales de Newton:
Mutationem motus proportionalem esse vi motrici impressæ, & fieri secundum lineam rectam qua vis illa imprimitur.
Esta ley explica qué ocurre si sobre un cuerpo en movimiento (cuya masa no tiene por qué ser constante) actúa una fuerza neta: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. En concreto, los cambios experimentados en el momento lineal de un cuerpo son proporcionales a la fuerza motriz y se desarrollan en la dirección de esta; las fuerzas son causas que producen aceleraciones en los cuerpos. Consecuentemente, hay relación entre la causa y el efecto, la fuerza y la aceleración están relacionadas. Dicho sintéticamente, la fuerza se define simplemente en función del momento que se aplica a un objeto, con lo que dos fuerzas serán iguales si causan la misma tasa de cambio en el momento del objeto.
En términos matemáticos esta ley se expresa mediante la relación:
Donde:
 es el momento lineal
es el momento lineal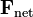 la fuerza total o fuerza resultante.
la fuerza total o fuerza resultante.
Suponiendo que la masa es constante y que la velocidad es muy inferior a la velocidad de la luz la ecuación anterior se puede reescribir de la siguiente manera:
Sabemos que  es el momento lineal, que se puede escribir m. V donde m es la masa del cuerpo y V su velocidad.
es el momento lineal, que se puede escribir m. V donde m es la masa del cuerpo y V su velocidad.
 es el momento lineal, que se puede escribir m. V donde m es la masa del cuerpo y V su velocidad.
es el momento lineal, que se puede escribir m. V donde m es la masa del cuerpo y V su velocidad.
Consideramos a la masa constante y podemos escribir  aplicando estas modificaciones a la ecuación anterior:
aplicando estas modificaciones a la ecuación anterior:
 aplicando estas modificaciones a la ecuación anterior:
aplicando estas modificaciones a la ecuación anterior:
La fuerza es el producto de la masa por la aceleración, que es la ecuación fundamental de la dinámica, donde la constante de proporcionalidad, distinta para cada cuerpo, es su masa de inercia. Veamos lo siguiente, si despejamos m de la ecuación anterior obtenemos que m es la relación que existe entre  y
y  . Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo.
. Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo.
 y
y  . Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo.
. Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo.Tercera Ley:
Es importante observar que este principio de acción y reacción relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley. Junto con las anteriores leyes, ésta permite enunciar los principios de conservación del momento lineal y del momento angular.
Con toda acción ocurre siempre una reacción igual y contraria: quiere decir que las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.
La formulación original de Newton es:
Actioni contrariam semper & æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales & in partes contrarias dirigi.
La tercera ley de Newton es completamente original y hace de las leyes de la mecánica un conjunto lógico y completo.9 Expone que por cada fuerza que actúa sobre un cuerpo, este realiza una fuerza de igual intensidad, pero de sentido contrario sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas, situadas sobre la misma recta, siempre se presentan en pares de igual magnitud y de dirección, pero con sentido opuesto.
 Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio, y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita "c".
Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio, y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita "c".
Experimento de la Primera Ley de Newton
Necesitas dos cajas de CDs y un hilo. Sólo debes atar con el hilo una de las cajas y ponerla sobre una mesa. A continuación, debes disponer la otra caja a cierta distancia de la primera. Por último, toma del hilo y arrastra la primer caja hacia la segunda. Notarás que la caja de CD golpea a la que está en reposo y provoca que ésta última se mueva. La ley en cuestión indica que un cuerpo que está en reposo cambiará de estado cuando es golpeado por una fuerza ajena, mientras que sino interviene una fuerza ajena seguirá en reposo.
Experimento de la Segunda Ley de Newton
En primer lugar, toma cualquier objeto de tamaño pequeño y poco peso. Átalo con un hilo o soga largo y déjalo sobre una superficie. A continuación, sólo debes halar de la soga fuerte y rápido. Mediante esta experiencia, comprobarás la segunda Ley de Newton: el objeto en cuestión (de poca masa) cae al suelo debido a la aceleración y fuerza que se ejerce sobre él. Entre más aceleración, más lejos irá el objeto. La aceleración depende de la masa y de la fuerza y viceversa.
Experimento de la Tercera Ley de Newton
Debes realizar el mismo procedimiento que en el experimento de la primera ley, con la diferencia que sobre una de las cajas de CD (la que permanece en reposo) pondrás un objeto relativamente pesado y sobre la otra (la que vas a mover con el hilo) un objeto de menor tamaño. Al realizar la experiencia, podrás notar que el objeto que está sobre la segunda caja se mueve cuando choca contra el objeto que está sobre la primer caja. La ley indica que toda acción tiene una reacción, razón por la cual el objeto de la segunda caja golpea al de la primera porque la reacción en ella es moverse, sin importar su peso o su masa.
Ejercicios Resueltos:
Problema n° 1) Se lanza un cuerpo verticalmente hacia abajo con una velocidad inicial de 7 m/s.
a) ¿Cuál será su velocidad luego de haber descendido 3 s?.
b) ¿Qué distancia habrá descendido en esos 3 s?.
c) ¿Cuál será su velocidad después de haber descendido 14 m?.
d) Si el cuerpo se lanzó desde una altura de 200 m, ¿en cuánto tiempo alcanzará el suelo?.
e) ¿Con qué velocidad lo hará?.
Datos:
v0 = 7 m/s
t = 3 s
y = 200 m
h = 14 m
Ecuaciones:
(1) vf = v0 + g.t
(2) y = v0.t + g.t²/2
(3) vf² - v0² = 2.g.h
a) De la ecuación (1):
vf = (7 m/s) + (10 m/s²).(3 s)
vf = 37 m/s
vf = 37 m/s
b) De la ecuación (2):
Δh = (7 m/s).(3 s) + (10 m/s²).(3 s)²/2
Δ h = 66 m
Δ h = 66 m
c) De la ecuación (3):
vf = √v0² + 2.g.h
vf = 18,14 m/s
d) De la ecuación (2):
0 = v0.t + g.t²/2 - y
Aplicamos la ecuación cuadrática que dará dos resultados:

t1 = 5,66 s
t2 = -7,06 s (NO ES SOLUCION)
e) De la ecuación (3):
vf = √v0² + 2.g.h
vf = 63,63 m/s
Problema n° 2) Se lanza un cuerpo verticalmente hacia arriba con una velocidad inicial de 100 m/s, luego de 4 s de efectuado el lanzamiento su velocidad es de 60 m/s.
a) ¿Cuál es la altura máxima alcanzada?.
b) ¿En qué tiempo recorre el móvil esa distancia?.
c) ¿Cuánto tarda en volver al punto de partida desde que se lo lanzo?.
d) ¿Cuánto tarda en alcanzar alturas de 300 m y 600 m?.
Datos:
v0 = 100 m/s
vf = 60 m/s
t = 4 s
y1 = 300 m
y2 = 600 m
Ecuaciones:
(1) vf = v0 + g.t
(2) y = v0.t + g.t²/2
(3) vf² - v0² = 2.g.h
a) Para la altura máxima vf = 0, de la ecuación (3):
-v0² = 2.g.h
h máx = -vf²/(2.g)⇒ h máx = -(100 m/s)²/[2.(-10 m/s²)]
h máx = -vf²/(2.g)⇒ h máx = -(100 m/s)²/[2.(-10 m/s²)]
h máx = 500 m
b) De la ecuación (1) y para vf = 0:
t = v0/g
t = (-100 m/s)/(-10 m/s²)
t = 10 s
c) Recordemos que en tiro vertical, cuando un objeto es lanzado hacia arriba y luego cae, cuando vuelve a pasar por el punto de partida posee la misma velocidad que en el momento del lanzamiento pero con sentido contrario (vf = -v0).
Podemos asegurar que el resultado pedido es el doble del tiempo que requirió para alcanzar la altura máxima.
t = 20 s
e) No puede alcanzar una altura de 600 m porque la máxima es de 500 m. Para h = 300 m empleamos la ecuación (2):
0 = v0.t + g.t²/2 - y
Aplicamos la ecuación cuadrática (Báscara) que dará dos resultados:

t1 = 3,67 s
t2 = 16,32 s
Problema n° 3) ¿De qué altura cae un cuerpo que tarda 4 s en llegar al suelo?
Datos:
t = 4 s
Ecuación:
Δh = g.t²/2
De la ecuación:
Δh = (10 m/s²).(4 s)²/2
Δh = 80 m
Δh = 80 m
Ejercicios para Resolver:
Problema n° 1) Se lanza una pelota hacia arriba y se recoge a los 2 s, calcular:
a) ¿Con qué velocidad fue lanzada?.
b) ¿Qué altura alcanzó?.
Problema n° 2) Si se deja caer una piedra desde la terraza de un edificio y se observa que tarda 6 s en llegar al suelo. Calcular:
a) A qué altura estaría esa terraza.
b) Con qué velocidad llegaría la piedra al piso.
Problema n° 3) A un cuerpo que cae libremente se le mide la velocidad al pasar por los puntos a y b, siendo estas de 25 m/s y 40 m/s respectivamente. Determinar:
a) ¿Cuánto demoró en recorrer la distancia entre a y b ?.
b) ¿Cuál es la distancia entre a y b ?.
c) ¿Cuál será su velocidad 6 s después de pasar por b ?.
Algunos otros Blogs con temas similares:
Autor: Sebastian Palau



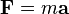
No hay comentarios:
Publicar un comentario